Вариант 6
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
В прямоугольнике ABCD проведена биссектриса AM. Найдите угол MAC (в градусах), если угол ABD равен 57°.
Для детского лагеря было закуплено 45 комплектов постельного белья, из них 15 — с героями мультфильмов, 21 — с абстрактным рисунком, а остальные — однотонные. Какова вероятность того, что случайно выбранному ребёнку достанется однотонный комплект?
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
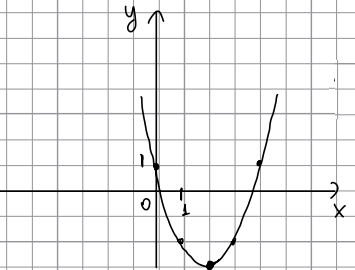
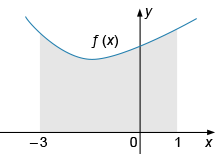
Найдите площадь фигуры, ограниченной графиком функции y = f(x), прямыми x = — 3, x = 1 и осью абсцисс, если F(x) = x3 - 4,5x2 + 12x — 5 — одна из первообразных функции f(x).
Период (в с) свободных колебаний пружинного маятника определяется по формуле T=2π√mk, где m — масса груза (в кг), k — жесткость пружины в (Н/м), π=3. Груз какой массы (в кг) нужно закрепить на пружине жесткостью 400 H/м, чтобы период колебаний составил 0,9 с?
Коля и Миша вышли навстречу друг другу из посёлков, расстояние между которыми равно 16 км, и встретились через 2 часа. Если бы Коля собрался к Мише в гости, он преодолел бы расстояние между посёлками за 3 часа 12 минут. Найдите скорость Миши (в км/ч).
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите точку минимума функции f(x)=0,5⋅62x+3−6x−1
Находим производную
f'(x)=62x+3ln6—6x-1ln6
Находим точки экстремума
62x+3ln6—6x-1ln6=0
62x+3=6x-1
2x+3=x-1
x=-4 — точка минимума
Дано уравнение log2cos2x(3−3sinx)=1.
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [13π2;8π].
А) ОДЗ:
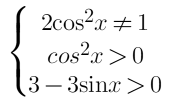 ⇒
⇒
⇒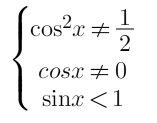
Преобразуем уравнение:
2cos2x=3−3sinx
2−2sin2x−3+3sinx=0
Пусть sinx=t
2t2−3t+1=0
t1=1 t2=12
Обратная замена:
sinx=12
x=(−1)nπ6+πn, n∈Z
sinx=1 - посторонний, т.к. противоречит ОДЗ
Б) Нанесем корни на числовую прямую и убедимся, какие корни входят в отрезок
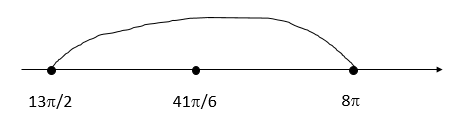
А) (−1)k⋅π6+πk,k∈Z
Б) 41π6
В основании прямой призмы ABCDA1B1C1D1 лежит равнобедренная трапеция ABCD с основаниями ВС и AD. Точка К - середина ребра ВВ1. Плоскость а проходит через середины ребер АВ и ВВ1 параллельно прямой B1D.
А) Докажите, что сечением призмы плоскостью α является равнобедренная трапеция.
Б) Найдите объем большей части призмы, на которые ее разбивает плоскость α, если известно, что ВС=7, AD=25, АВ=15, ВВ1=8.
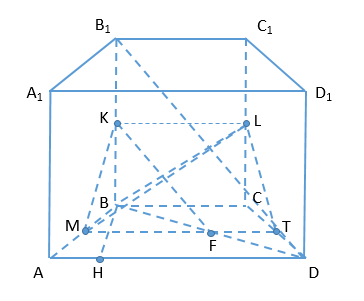
А) Пусть M - середина AB. Тогда α∩(ABB1)=MK
Проведем B1D;BD;KF∥B1D, тогда α∩(ABC)=MT, где F∈MT. Точка K-середина BB1, KF∥B1D⇒F - середина BD и MF - средняя линия △ABD⇒MT∥AD∥BC. Тогда MT∥(BCC1) и α∩(BCC1)=KL∥BC.
α∩(DCC1)=LT;MKTL=α - сечение.
Имеем KL∥BC∥MT;KL=BC≠MT⇒MKLT - трапеция. А так как △MBK=△TCL по двум катетам, то MK=TL и MKLT - равнобедренная трапеция.
Б) Vпризмы=SABCD⋅AA1, BH - высота ABCD; AH=25−72=9, тогда BH=12, SABCD=25+72⋅12=192;Vпризмы=192⋅8=1536
Плоскость α разбивает призму на две части, меньшая из которых многогранник MBKTCL. Плоскость MBL разбивает этот многогранник на две пирамиды LMBCT и MBKL, объемы которых обозначим V1 и V2 соответственно.
V1=13SMBCT⋅CL;CL=4;MBCT - трапеция, высота которой h=BH2=6;MT=AD+BC2=16, тогда V1=13⋅7+162⋅6⋅4=92
V2=13⋅SBKL⋅ρ(M;(BKL));SBKL=12BK⋅BC=12⋅7⋅4=14
AD∥(BKL);H∈AD⇒ρ(A;(BKL))=ρ(H;(BKL))=BH=12
M - середина AB, тогда ρ(M,(BKL))=ρ(A;(BKL))2=BH2=6 и V2=13⋅14⋅6=28
V=Vпризмы−(V1+V2)=1536−(92+28)=1416
Ответ: 1416
Решите неравенство 8x−3⋅22x+1+2x+3+14x−3⋅2x+1+8≥2x−1.
Преобразуем неравенство:
23x−6⋅22x+8⋅2x+1−2x(22x−6⋅2x+8)+22x−6⋅2x+822x−6⋅2x+8≥0
1+22x−6⋅2x+822x−6⋅2x+8≥0
Пусть 2x=t. Тогда
t2−6t+9t2−6t+8≥0
(t−3)2t2−6t+8≥0
Нули числителя: t=3 - корень кратности 2
Нули знаменателя: D=36−32=4
t1=6+22=4 t2=6−22=2
Нанесем на числовую прямую и расставим знаки:
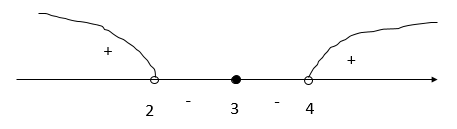
Обратная замена:
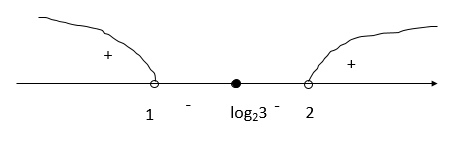
Ответ: (−∞;1)∪{log23}∪(2;+∞)
Некоторое предприятие приносит убытки, составляющие 300 млн. руб. в год. Для превращения его в рентабельное было предложено увеличить ассортимент продукции. Подсчеты показали, что дополнительные доходы, приходящиеся на каждый новый вид продукции, составят 84 млн. руб. в год, а дополнительные расходы, окажутся равными 5 млн. руб. в год при освоении одного нового вида, но освоение каждого последующего потребует на 5 млн. руб. в год больше расходов, чем освоение предыдущего. Какое минимальное количество видов новой продукции необходимо освоить, чтобы предприятие стало рентабельным? Какой наибольшей годовой прибыли может добиться предприятие за счёт увеличения ассортимента продукции?
Из условия видно, что решение задачи связано с арифметической прогрессией, где a1=84−5=79, d=−5,Sn≥300
Найдем Sn и запишем уравнение, когда сумма арифметической прогрессии равна 300 млн рублей,т.е полностью покрывает расходы.
Sn=2a1+d(n−1)2⋅n=163n−5n22=300
5n2−163n+600=0
D=1632−5⋅4⋅600=14569
n1≈4.13, n2≈28.37
т.к. n - целое число и n- наименьшее, то n1=5
Предприятие будет иметь наибольшую годовую прибыль, если an>0, т. е 79−5(n−1)>0
n<16.8 , значит n=16 - наибольшее количество видов новой продукции
Посчитаем сумму арифметической прогрессии для n=16
S16=(158−75)⋅8=664
Наибольшая годовая прибыль: 664−300=364(млнруб)
Ответ: 5; 364 млн. руб.
Хорда АВ окружности параллельна касательной, проходящей через точку С, лежащую на окружности. Прямая, проходящая через точку С и центр окружности, вторично пересекает окружность в точке Р.
А) Докажите, что треугольник АВР равнобедренный.
Б) Найдите отношение, в котором хорда АВ делит диаметр СР, если известно, что ∠APB = 150°.
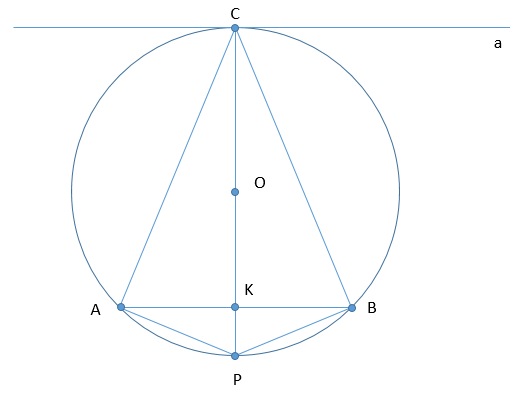
А) Пусть a - касательная, данная по условию. a⊥OC (по свойству касательной к окружности)⇒a⊥CP, CP∩AB=K
a⊥CP;a∥AB⇒AB⊥CP
По свойству хорды, т.к. AB⊥CP;AB - хорда ⇒AK=KB
т.к. AK=KB;∠AKB=∠PKB=90∘;CK - общий ⇒△ACK=△CKB⇒AP=PB⇒△APB - равнобедренный, ч.т.д.
Б) ∠PBC=90∘, т.к. вписанный и опирается на диаметр
Т.к. △APK=△BPK, ∠APK=∠BPK=150∘2=75∘
∠PCB=180∘−75∘−90∘=15∘
△CKB: CK=KB⋅ctg15∘=KB⋅ctg(45∘−30∘)=KB⋅√3+1√3−1
△PKB: KP=KB⋅ctg75∘KB⋅tg15∘=KB⋅√3−1√3+1
CKPK=(√3+1)2(√3−1)2=2+√32−√3
Ответ: CKPK=2+√32−√3
Уравнение 2x3 + ax2 + Ьх + c = 0 с целыми коэффициентами имеет три различных корня. Оказалось, что первый корень является синусом, второй - косинусом, а третий - тангенсом одного и того же угла. Найдите все такие уравнения.
Зная корни уравнения, можно преобразовать уравнение в произведение:
2x3+ax2+bx+c=2(x−sinα)(x−cosα)(x−tgα)
Причем x1=cosx≠0, т.к. тогда x3=0 ; x2≠0, т.к тогда x3∄
После раскрытия скобок получаем: 2x3+2x2(−cosα−sinα−tgα)+2x(sinαcosα+sinα+sinαtgα)+(−2sin2α)=2x3+ax2+bx+c
Значит a=2(−cosα−sinα−tgα);b=2(sinαcosα+sinα+sinαtgα);c=−2sin2α
sin2α=−c2, исходя из того что по условие коэффициенты- целые числа и sin2α≥0, получим три возможных варианта: c=−2;−1;0
1) c=−2;sin2x=1⇒cosx=0 - противоречит условию задачи.
2) c=−1;sin2x=12 - удовлетворяет условию
3) c=0;sin2x=0 - не удовлетворяет условию
Значит c=−1, т.е sinα=√22;cosα=√22;tgα=1 или sinα=−√22;cosα=√22;tgα=−1
Первый вариант - посторонний, т.к тогда a=2(−√22−√22−1) - не целое число, что противоречий условию
При втором варианте после подстановки значений: a=2;b=−1;c=−1
Ответ: 2x3+2x2-x-1=0
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||